Sewer Pipe LED Projector
Rationale
Efficiency maximized with parabolic reflector and secondary lens.
Adjunct page to this related article.
There are two issues to consider when building a lens-based projector for free-space optical communications: dispersion angle (also called beam angle) and efficiency.
Dispersion angle:
The angle of the beam projected by a lens is proportional to the diameter of the light source (d) and inversely proportional to the distance from the light source to the lens (D). The relationship is shown below:
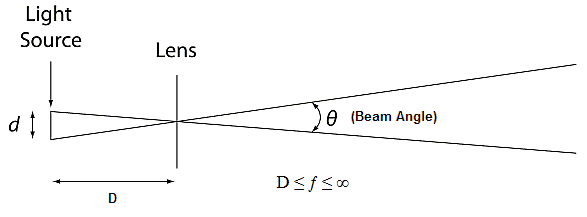
A smaller light source (d) produces a narrower beam. A greater source-to-lens distance (D) also produces a narrower beam. The relationship is defined by:
Lens-to-source distance is closely related to the focal length of the lens. If the purpose of the lens is to project a focused image, the correct light source-to-lens distance is the focal length (f) of the lens, ie, D = f. If the purpose of the lens system is to optimize efficiency, that is, to produce the most powerful beam, not necessarily focused, the relationship of D to f is a less straightforward. Source dispersion angle and lens diameter must be taken into account.
Efficiency:
The efficiency of the projection system is the proportion of light energy produced by the source actually projected in the beam. Efficiency can be expressed numerically as the angle subtended by the projection lens divided by the dispersion angle of the source (x100 to put it in percentage terms). So, for example, if the dispersion angle of the source is 360 degrees and the angle subtended by the projection lens is 36 degrees, the efficiency of the system is (36/360) x 100 = 10%. Larger diameter lenses at a given distance subtend larger angles, therefore are more efficient.
Efficiency and f-number:
The efficiency with which a lens projects light from a dispersed source is related to it's f-number. The f-number (also called f/N) is the ratio of a lens's focal length (f) to its diameter. The smaller the f-number (ie, the larger the diameter relative to the focal length) the greater the lens's ability to concentrate a dispersed source and the higher its efficiency. In the case of a high-intensity LED, for reasonable efficiency the lens should be able to accommodate the half-power light dispersion angle of the specified LED. The relationship is:
A "too-small" lens (f-number > f/Nmax) will be less than optimally efficient. Conversely, as lens diameter is increased to the point of being "too-large" (f-number <f/Nmax) it will begin to produce diminishing returns and any further increase in lens diameter will be in a sense be "wasted".
Efficiency equation applied to the Sewer Pipe LED Projector project:
Substituting 100° (the dispersion angle for the LED used in this project) for θled in the above equation [2], maximum f/N calculates to 0.42, that is, the lens's focal length should be no greater than about 0.4 times its diameter. As lenses go, this is a very low f-number (very large lens spaced very close to the light source).
The usual way to achieve very low f-numbers without excessive lens thickness and weight is with some form of Fresnel lens. This projector takes a hybrid approach. It uses a concentrating "lens" (it looks like a parabolic reflector to me; parabolic reflectors are another way to achieve very short focal lengths) to "pre-narrow" the dispersion angle of the stock LED. This lens (Ledil CA10324_Rocket-SS), narrows the dispersion angle to 8 degrees (according to its datasheet). The decrease in dispersion angle from 100° to 8° comes with an increase in the apparent diameter of the source - from about 2mm to 25mm.
Plugging this value (8°) into the above equation [2] produces an f/Nmax of about 7.1, a number much easier to achieve with commonly available lenses. The secondary lens used in this project is a surplus eyeglass blank available from All Electronics. The lens is described on the vendor's website as 73mm diameter, 3.5 power. Lens power (in diopters) is the reciprocal of the lens's focal length in meters. Thus, the 73mm, 3.5 power lens has a focal length of 1/3.5, or 286mm, for an f-number of 286/73 = 3.9, well within the required f/Nmax calculated above, and with a focal length large enough to make up for the larger apparent diameter of the source. The mounted lens is partially "stopped" by its mounting ring to about 70mm diameter, so actual f/N is about 4.1. The mounted lens still falls into "too-large" territory for this application (but, hey, it was cheap).
Secondary lens spacing:
For optimal efficiency the secondary lens is positioned at the distance where the outer rays produced by the calculated "just-right" f/Nmax secondary lens touch the perimeter of the primary lens. When properly positioned, the secondary lens is focused on a virtual source behind the face of the primary lens as shown below. In other words, the virtual source lies at the focal point (plane actually) of the secondary lens. Its longer focal length gives the secondary lens the power to further narrow the beam from the light source.
Virtual Source
angle not to scale
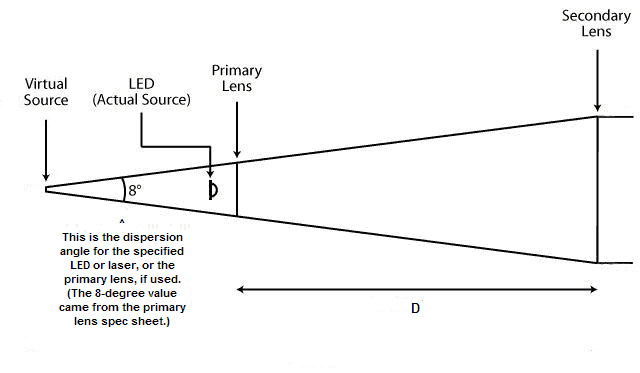
As a practical matter it is not necessary to determine the position of the virtual source, it's only necessary to equip the system with a secondary lens of sufficiently low f-number, as discussed above, and position it the correct distance from the primary lens. The distance the secondary should be spaced from the primary is calculated as follows:
Substituting the diameter of the primary lens used in the project (25mm) and the calculated maximum secondary f/N (7.1), the primary to secondary distance (D) calculates to 178mm. By default then, the virtual point source is 108mm behind the primary lens [286 - 178 = 108].
With the secondary lens properly spaced, the projected spot (onto a sheet of white paper a few meters away) should appear fully filled in and uniformly illuminated. A "focused" image should not appear. A higher intensity area may appear in the center of the spot. This is caused by light coming directly from the LED (not reflected by the primary lens). See: Adjusting the Pointing Scope.
Effect of the secondary lens on beam intensity and dispersion angle of the as-built projector:
The apparent diameter of the light source (as viewed by a distance observer) has been increased from 25mm (the diameter of the primary lens) to 70mm (the diameter of the secondary lens). Intensity of the projected light beam increases by a factor of (70/25)2 = 7.8 over that of the primary lens alone. Beam angle has been narrowed, from 8° to less than 1°, per equation [1].
Effect of the secondary lens on efficiency of the as-built projector:
Since the dispersion angle (8°) of the "pre-narrowed" source is completely subtended (and then some) by the secondary lens, numerically at least, the system could be thought of as being "100% efficient". It is not, of course. In the real world, transmission losses, losses caused by misalignment, and spurious light emitted from the source (beyond the half-power point), prevent that.
The bottom line:
If the narrowest beam width with the highest efficiency is desired, select a light source with the smallest possible radiating surface, then select the longest available focal length lens or combination of lenses having an f-number equal to or less than the f/Nmax value calculated above. If the calculated f/Nmax and f can be achieved with a single lens or parabolic reflector, a secondary lens will not be beneficial.